Quantum Mechanics หรือ กลศาสตร์ควอนตัม เป็นทฤษฎีทางฟิสิกส์เพื่ออธิบายพฤติกรรมของสสารที่มีขนาดเล็กในระดับอะตอม สิ่งที่มีขนาดเล็กเช่นนี้ มีคุณสมบัติและพฤติกรรมที่แตกต่างจากสิ่งที่เราพบเห็น ในชีวิตประจำวันอย่างสิ้นเชิง วัตถุขนาดจิ๋วดังกล่าว จะมีสมบัติเป็น “อนุภาค” ก็ไม่ใช่ จะเป็น “คลื่น” ก็ไม่เชิง
อิเล็กตรอนที่เราเคยคิดว่าเป็น “อนุภาค” เพราะเมื่อมีอิเล็กตรอน เพียง 1 อนุภาค จะปรากฏเป็นจุด 1 จุดบนแผ่นฟิล์ม แต่เมื่อมีอิเล็กตรอนอยู่เป็นจำนวนมาก มันกลับมีสมบัติเป็น “คลื่น” คือ มีการแทรกสอด การหักเห และปรากฏบนแผ่นฟิล์มราวกับว่าเป็นคลื่นชนิดหนึ่ง

สัมภาษณ์นักเขียน
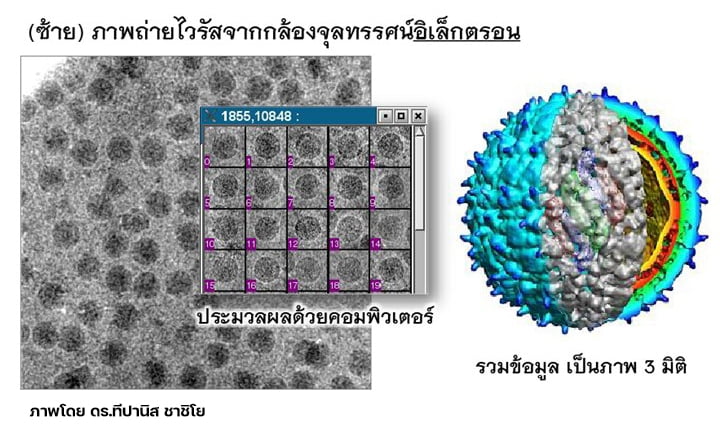
โดยทั่วไปคลื่นแสง มีการเลี้ยวเบนผ่านเลนส์ จึงสามารถประยุกต์ใช้เป็นกล้องจุลทรรศน์ สมบัติความเป็นคลื่นของอิเล็กตรอนก็เช่นเดียวกัน เราสามารถนำมาสร้างเป็นกล้องจุลทรรศน์ที่มีกำลังขยายสูงมากเรียกว่า “กล้องจุลทรรศน์อิเล็กตรอน”
หนังสือเล่มนี้ มาพร้อมกับการบรรยายออนไลน์และเฉลยการบ้านที่ผู้อ่านสามารถดาวน์โหลดได้ฟรีเรียบเรียงจากประสบการณ์การสอนวิชาควอนตัมระดับปริญญาโทและเอกกว่า 10 ปี ทำให้มีเนื้อหา ความครบถ้วน และนำเสนอในมุมที่ลึกซึ้งหลากหลาย มีการบุกเบิกทางวิชาการ สร้างองค์ความรู้ใหม่ที่ทันสมัย จากงานวิจัยของผู้แต่งที่สำคัญๆ ในสาขาวิชา ยกตัวอย่างเช่น บทที่ 10 Density Functional Theory หรือบทที่ 11 สมการชาชิโย เป็นประโยชน์ในการต่อยอด และส่งผลกระทบทางวิชาการในวงกว้าง เป็นที่ยอมรับทั้งในและต่างประเทศ
ในแง่ของเนื้อหาและลักษณะของการเรียบเรียงนั้น เน้นหนักในการอธิบายความและยกตัวอย่าง ที่หลากหลาย โดยมีความสมบูรณ์และความเข้มของเนื้อหา อยู่ในระดับเดียวกับตำรามาตรฐาน เช่น “The Feynman Lectures on Physics” (Feynman), “A Modern Approach to Quantum Mechanics” (Townsend), และ “Modern Quantum Mechanics” (Sakurai) แต่มีลักษณะการอธิบายความที่เรียบเรียงให้เข้าใจง่ายขึ้น และตัวอย่างที่หลากหลายมากขึ้น
เนื้อหาภายในเล่มมีทั้งหมด 11 บท ประกอบไปด้วย
1. ตัวแปรพื้นฐานของกลศาสตร์ควอนตัม
ธรรมชาติของสิ่งที่มีขนาดเล็กในระดับอะตอม ที่มีสมบัติเป็นทั้งคลื่นและอนุภาคในขณะเดียวกันนี้เอง ได้สร้างความสงสัยให้กับนักฟิสิกส์ในยุคนั้น เป็นอย่างมาก
จากการทุ่มเทศึกษาของนักวิทยาศาสตร์เมื่อราว 100 ปีก่อน ข้อมูลที่เกี่ยวข้องกับพฤติกรรมของอะตอมและสิ่งต่าง ๆ ที่มีขนาดเล็กระดับอะตอมได้ถูกสะสมมาอย่างต่อเนื่อง ข้อมูลดังกล่าวทำให้นักวิทยาศาสตร์ได้เห็นความแปลกประหลาดในทางฟิสิกส์ของสิ่งที่มีขนาดเล็ก
ต่อมาในช่วงปี ค.ศ. 1926 และ ค.ศ. 1927 นักฟิสิกส์ 3 ท่าน คือ Schrödinger, Heisenberg, และ Born ก็สามารถรวบรวมพฤติกรรมเหล่านี้ กำเนิดเป็นกลศาสตร์ควอนตัม ซึ่งในบทที่ 1 เราจะได้กล่าวถึงประเด็นหลัก ๆ ของทฤษฎี ที่นักฟิสิกส์ 3 ท่านนี้ได้ค้นพบ

2. Operator และ Matrix Mechanics
ฟิสิกส์คงจะเป็นเรื่องที่น่าเบื่อ ถ้าสถานะของระบบที่เราต้องการศึกษานั้นหยุดนิ่งอยู่กับที่ และไม่มีการเปลี่ยนแปลงใด ๆ เลย หากแต่ในความเป็นจริงแล้วกลศาสตร์ควอนตัมเต็มไปด้วยการเปลี่ยนแปลง จากสถานะหนึ่งไปยังอีกสถานะหนึ่งอย่างไม่หยุดนิ่ง
ในบทที่ 1 ที่ได้กล่าวไปแล้วนั้น ก็เพื่อให้นักศึกษาสามารถที่จะอธิบายสถานะของระบบโดยใช้ระเบียบวิธีของกลศาสตร์ควอนตัม หากแต่การที่เราสามารถอธิบายว่าระบบอยู่ในลักษณะอย่างไรนั้น ไม่เพียงพอในการศึกษาฟิสิกส์ มีความจำเป็นที่จะต้องมีระเบียบแบบแผน ที่สามารถควบคุมหรือเปลี่ยนแปลงสถานะของระบบนั้น ๆ ได้ด้วย ในบทที่ 2 นี้ เราจะมาเริ่มศึกษากลไกหรือกระบวนการที่ทำให้เกิดการเปลี่ยนแปลง จากสถานะเริ่มต้น ไปเป็นสถานะผลลัพธ์ หรือที่เรียกว่า Operator นั่นเอง
3. Angular Momentum
ลักษณะการเคลื่อนที่ ที่สำคัญอันหนึ่งในทางฟิสิกส์ ก็คือการหมุน ปริมาณทางฟิสิกส์ที่เราใช้ ในการอธิบายพฤติกรรมของอนุภาคที่เกี่ยวข้องกับการหมุนนั้น เรียกว่า Angular Momentum
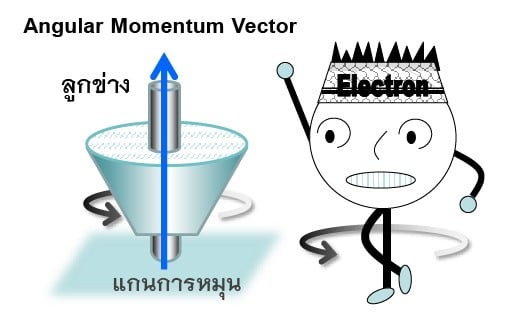
ในกลศาสตร์คลาสสิก โมเมนตัมเชิงมุม หรือ Angular Momentum เป็นปริมาณเวคเตอร์ ซึ่งหากจะตีความโดยอนุโลมแล้ว เวคเตอร์อันนี้ คือ แกนของการหมุน ดังแสดงในภาพ 3.1 ที่ลูกข่างกำลังหมุนตัวและ ถ้าพิจารณาทิศทางของการหมุนตามกฎมือขวา มันจะมีเวคเตอร์โมเมนตัมเชิงมุม ชี้ขึ้นในแนวดิ่งนั่นเอง
4. Time Evolution
วัตถุประสงค์หลักอันหนึ่งของการศึกษาฟิสิกส์ ก็คือความสามารถในการทำนายสิ่งที่จะเกิดขึ้น ในอนาคต หรือการศึกษาปริมาณทางฟิสิกส์ที่เปลี่ยนแปลงไปกับเวลา เพราะฉะนั้นในบทที่ 4 นี้ เราจะกล่าวถึงระเบียบวิธีในทางกลศาสตร์ควอนตัม ที่จะเป็นกลไกในการศึกษาว่าสถานะต่าง ๆ นั้น จะมีการเปลี่ยนแปลงไปกับเวลาอย่างไร
5. Interaction ของ Spin
ประกอบไปด้วยเนื้อหาของ 1. Hyperfine Splitting 2. Two Spin Particles 3. EPR Paradox และ 4. การรวมกันของ Angular Momentum
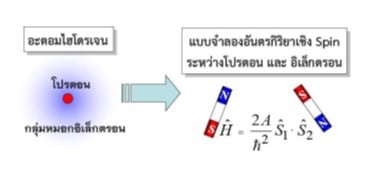
นอกจากนี้ ยังมีอันตรกิริยาอีกประเภทหนึ่งที่เกิดจาก Magnetic Moment ของอนุภาคทั้งสอง ซึ่งมีชื่อเรียกโดยทั่วไปว่า Hyperfine Interaction ทั้งนี้ เนื่องจากอิเล็กตรอนและโปรตอนต่างก็เป็นอนุภาคที่มี Spin s = 1/2 ทำให้มี Magnetic Moment เป็นของตัวเอง และเมื่ออยู่ในบริเวณใกล้เคียงกันภายในอะตอม จึงมีอันตรกิริยาระหว่างกันคล้ายกับแท่งแม่เหล็กสองแท่ง ดังในภาพ 5.1
6. Wave Mechanics in One Dimension
ประกอบไปด้วยเนื้อหาของ 1. Wave Function และ Position Eigenstate 2. Generator of Translation 3. Momentum Operator 4. Free Particle และ Gaussian Wave Packet 5. Heisenberg Uncertainty Principle 6. Schrödinger Equation 7. Square Well Potential 8. Scattering in One Dimension 9. Ehrenfest Theorem
7. Harmonic Oscillator
ในบทที่ผ่านมา เราได้ศึกษาระบบใน 1 มิติโดยใช้กลศาสตร์ควอนตัม ซึ่งก็มีลักษณะของพลังงานศักย์ V(x) แตกต่างกันออกไป เช่น Free Particle , V(x) = 0 บ่อพลังงานศักย์, และกำแพงศักย์ เป็นต้น ในบทที่ 7 นี้ เราจะใช้เวลาทั้งหมดกับการศึกษาพลังงานศักย์แบบซิมเปิลฮาร์มอนิกใน 1 มิติ (Harmonic Potential) ดังแสดงในภาพ 7.1a ซึ่งมีรูปแบบทางคณิตศาสตร์เป็นฟังก์ชันแบบพาราโบลา กล่าวคือ

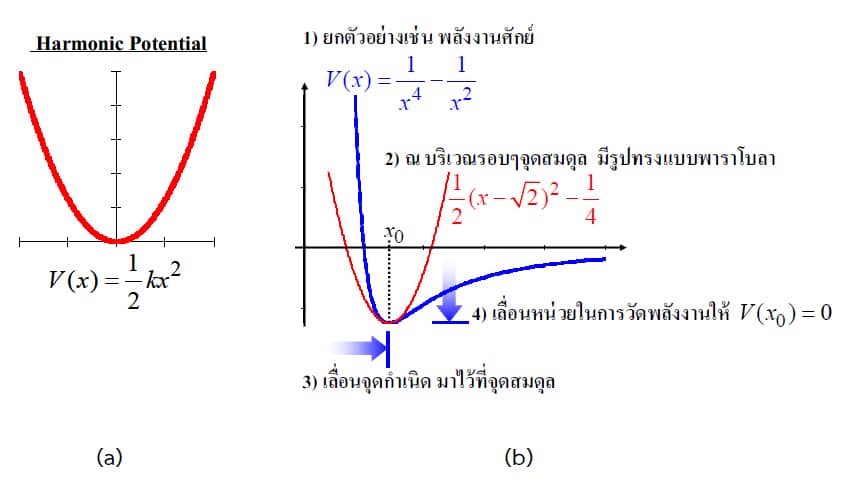
รูปแบบต่าง ๆ โดยทั่วไปแล้วเมื่อพิจารณา ณ บริเวณรอบ ๆ จุดสมดุล เราสามารถ
ประมาณได้ว่าพลังงานศักย์ มีลักษณะเป็นพาราโบลา
8. Central Potential
ระบบทางฟิสิกส์จำนวนไม่น้อย ที่อยู่ภายใต้อิทธิพลของพลังงานศักย์ซึ่งมีความสมมาตรในแนวรัศมียกตัวอย่างเช่น อะตอมซึ่งประกอบด้วยอิเล็กตรอนและนิวเคลียส โดยที่อิเล็กตรอนจะอยู่ภายใต้อิทธิพลของแรงคูลอมบ์ระหว่างประจุลบของตัวมัน และประจุบวกของโปรตอนที่อยู่ในนิวเคลียส หรือเขียนให้อยู่ในรูปของสมการได้ว่า
เมื่อ Z คือ Atomic Number ของนิวเคลียส ซึ่งแสดงถึงจำนวนของโปรตอนที่บรรจุอยู่ภายใน และ r คือระยะทางระหว่างอิเล็กตรอนและนิวเคลียส โดยที่เรากำหนดให้นิวเคลียสของอะตอมอยู่ ณ จุดกำเนิดพอดี จากสมการ (8.1) จะเห็นว่าพลังงานศักย์ดังกล่าวขึ้นอยู่กับระยะทางของอนุภาคจากจุดกำเนิดเพียงเท่านั้นเราเรียกระบบที่อยู่ภายใต้อิทธิพลของพลังงานศักย์เช่นนี้ว่า Central Potential และจะเป็นประเด็นหลักของเนื้อหาในบทนี้
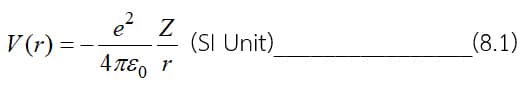
9. Time Independent Perturbation
เนื้อหาในทุก ๆ กรณีที่ผ่านมา ถึงแม้บางครั้งจะเป็นไปด้วยความยากลำบากอยู่บ้าง แต่ก็สามารถนำกระบวนการทางคณิตศาสตร์เข้ามาทำการวิเคราะห์หา Eigen Energy และ Eigenstate ของระบบได้อย่างแม่นยำ ยกตัวอย่างเช่น Precession ของ Spin, Finite Potential Well, Harmonic Potential, หรือแม้กระทั่ง Central Potential ใน 3 มิติ
วิธีในการคำนวณระดับพลังงานของระบบที่แตกต่างกันเหล่านี้ ก็มีกลไกที่คล้ายคลึงกัน กล่าวคือ กำหนด Hamiltonian ของระบบ จากนั้นสร้างสมการ Eigen
10. Density Functional Theory
ในหลายบทที่ผ่านมาเราได้เห็นการนำควอนตัมมาประยุกต์ใช้กับวิทยาศาสตร์สาขาต่าง ๆ เช่น สาขาดาราศาสตร์ ที่ใช้ Hyperfine Interaction ในการค้นพบรูปร่างก้นหอยของกาแลกซีทางช้างเผือก สาขาการแพทย์ที่ใช้ Magnetic Resonance ในการถ่ายภาพ MRI ในบทนี้ เราจะได้ศึกษาทฤษฎี DFT ซึ่งเป็นการนำควอนตัมมาประยุกต์ใช้กับสาขาฟิสิกส์ของสสารควบแน่น เคมี และวัสดุศาสตร์
11. สมการชาชิโย
จากที่ได้อธิบายประโยชน์ และอิทธิพลทางวิชาการในวงกว้างของสมการชาชิโย ต่อสาขา Density Functional Theory ไปแล้วนั้น ในบทนี้จะเจาะลึกไปที่ตรรกะทางคณิตศาสตร์ที่ใช้สร้างสมการ ซึ่งสามารถอธิบายธรรมชาติของอิเล็กตรอนในสสารทั่วไป ได้อย่างแม่นยำ (Chachiyo, 2016; Chachiyo, 2020a; Chachiyo, 2020b) โดยจะใช้หน่วย Atomic Unit ในการบรรยาย
สมการชาชิโย ประกอบด้วย 3 ส่วน ที่อธิบายพลังงาน Exchange และ Correlation ของระบบหลายอิเล็กตรอน ส่วนแรกตีพิมพ์ในปี ค.ศ. 2016 คือ กรณีพิเศษที่อิเล็กตรอนมีความหนาแน่นคงที่ ส่วนที่สองตีพิมพ์ในปี ค.ศ. 2020 โดย T. Chachiyo และ H. Chachiyo คือ พลังงาน Correlation กรณีทั่วไป และพลังงาน Exchange กรณีทั่วไป ในปีเดียวกัน เมื่อผนวกทั้งสามส่วน จึงเกิดเป็นสมการที่คำนวณพลังงานรวมของอิเล็กตรอนได้โดยสมบูรณ์
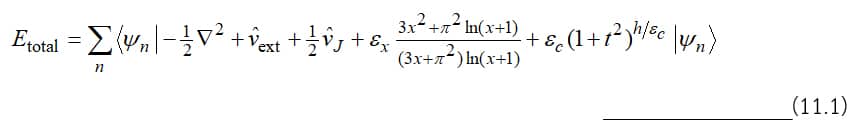
เพื่อไม่ให้ซ้ำซ้อนกับเนื้อหาที่ได้ถูกตีพิมพ์ไปแล้ว เราจะเน้นไปที่การขยายความประเด็นทางฟิสิกส์ ที่สำคัญ ๆ ซึ่งจะได้อธิบายในรายละเอียด ดังนี้
11.1 พลังงาน Correlation กรณีพิเศษ
11.2 พลังงาน Correlation กรณีทั่วไป
11.3 พลังงาน Exchange
หนังสือเล่มนี้ยังเหมาะกับครู นิสิต และอาจารย์ ผู้ผ่านวิชากลศาสตร์ควอนตัมพื้นฐานมาแล้ว และต้องการศึกษาให้ลึกจนสามารถผนวกเอาคณิตศาสตร์มาเป็นเครื่องมือในการทำความเข้าใจทฤษฎี ทำงานวิจัย หรือประกอบการเรียนการสอนให้เข้มข้นมากยิ่งขึ้น

รองศาสตราจารย์ ดร.ทีปานิส ชาชิโย
อาจารย์ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยนเรศวร
Lecture Video & Homework Solution



