แคลคูลัส 3 (Calculus III)

แคลคูลัส 3 มีเนื้อหามุ่งเน้นไปยังความรู้เรื่องการเปลี่ยนพิกัด จากระบบพิกัดฉากเป็น ระบบพิกัดเชิงขั้ว พิกัดทรงกระบอก และพิกัดทรงกลม และการหาอนุพันธ์และปริพันธ์ของฟังก็ชัน หลายตัวแปร รวมทั้งการประยุกต์ของสมการเชิงอนุพันธ์และปริพันธ์ ซึ่งเป็นพื้นฐานต่อการศึกษา ขั้นสูงทางด้านคณิตศาสตร์ประยุกต์และทางวิศวกรรมศาสตร์ รวมทั้งการประยุกต์ในสาขาต่าง ๆ ที่เกี่ยวข้อง

โดยตำราเล่มนี้ได้เน้นการแสดงตัวอย่างในหลายรูปแบบและประยุกต์การใช้โปรแกรม รหัสเปิดจีโอจีบา (Geogebra) ในการแสดงกราฟเพื่อง่ายต่อการเข้าใจ เพื่อให้ผู้เรียนสามารถ มองภาพได้ง่ายขึ้นและสามารถเรียนรู้ด้วยตัวเองเพิ่มเติมได้ ซึ่งผู้พัฒนาตำราเล่มนี้หวังไว้อย่างยิ่ง ว่าจะเป็นประโยชน์ต่อการศึกษาในรายวิชาแคลคูลัสส่วนที่ 3 และสำหรับผู้ที่สนใจ

1. ระบบพิกัดเชิงขั้ว (Polar Coordinate System)

ในบางครั้งการแก้ปัญหาต่าง ๆ ในระบบพิกัดฉากนั้นอาจมีความซับซ้อน และต้องใช้ วิธีการแก้ปัญหาหลายขั้นตอน ซึ่งในการแปลงพิกัดจากระบบพิกัดฉากเป็นระบบพิกัดเชิงขั้วนั้น อาจทำให้ปัญหาที่มีความซับซ้อน กลายเป็นปัญหาที่ง่ายกว่าได้ สังเกตจากการแปลงพิกัดดังนี้

ระบบพิกัดเชิงขั้ว (Polar Coordinate System)

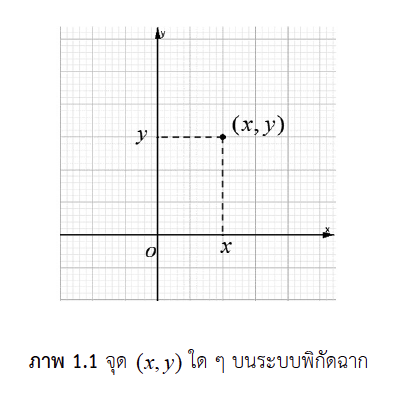
ในระบบพิกัดฉาก จุด (x. y) ใด ๆ บนระบบพิกัดฉากนั้น สามารถแสดงได้ดังภาพ 1.1 โดยที่แกนนอน คือ แกน x และแกนตั้ง คือ แกน y

2. สมการเชิงอนุพันธ์อันดับหนึ่ง (First Order Differential Equations)

ในโลกของความเป็นจริงนั้นหลายสิ่งหลายอย่างมีความเชื่อมโยงกัน การเปลี่ยนแปลงของ บางสิ่งมีผลกระทบต่ออีกสิ่ง เช่น ผู้ล่ากับผู้ถูกล่า ประชากรของทั้งสองสิ่งนี้มีความเชื่อมโยงกัน ถ้าประชากรของผู้ถูกล่ามีปริมาณมาก ก็ถือว่าเป็นแหล่งอาหารอันอุดมสมบูรณ์ของผู้ล่า ซึ่งทำให้ปริมาณ ของผู้ล่าเพิ่มขึ้นตามไปด้วย แต่เมื่อเวลาผ่านไปจำนวนของเหยื่อไม่สามารถเติบโตได้ทันกับจำนวน ของผู้ล่าที่เพิ่มขึ้นได้ จึงทำให้เกิดการขาดแคลนอาหารในระบบ ดังนั้น ผลที่เกิดขึ้น คือ จำนวนผู้ล่าลดลง ด้วยสาเหตุต่าง ๆ เช่น การฆ่ากันเองระหว่างผู้ล่า หรือขาดอาหารตาย คณิตศาสตร์สามารถอธิบาย ปรากฏการณ์นี้ได้ ซึ่งสมการอย่างง่ายที่คุ้นเคยกันก็คือ สมการเชิงอนุพันธ์ (differential equations) ในบทนี้จะศึกษา สมการเชิงอนุพันธ์อันดับหนึ่ง (fist order differential equations)

3. สมการเชิงอนุพันธ์เชิงเส้นอันดับสูง (Higher Order LinearDifferential Equations)

ในเนื้อหาส่วนนี้จะพิจารณาการหาผลเฉลยของสมการเชิงอนุพันธ์อันดับที่มากกว่าสอง ที่เป็นเชิงเส้น ซึ่งมีความสำคัญอย่างมากในการประยุกต์ใช้ในสาขาวิชาต่าง ๆ ก่อนที่จะเข้าสู่การหา ผลเฉลยของสมการเชิงอนุพันธ์อันดับต่าง ๆ จะขอนำเสนอทฤษฎีบทที่สำคัญก่อน ดังนี้

ทฤษฎีบท 3.1 กำหนดให้ p(x). q(x) และ g(x) เป็นฟังก์ชันต่อเนื่องบนช่วง (a,b) และให้ x₀ อยู่ในช่วง (a,b) แล้วปัญหาค่าเริ่มต้น

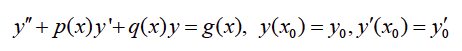
มีผลเฉลยเพียงหนึ่งเดียวบนช่วง (a, b)

ทฤษฎีบท 3.2 กำหนดให้ y₁(x) และ y₂(x) เป็นผลเฉลยของสมการ

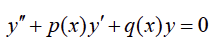
ที่หาค่าได้บนช่วง a < x < b โดยที่ p(x) และ q(x) ต่อเนื่องบนช่วง (a,b) แล้วสำหรับ ค่าคงที่ c₁ และ c₂ ใด ๆ ผลรวมเชิงเส้น (linear combination)

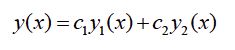
เป็นผลเฉลยของสมการเชิงอนุพันธ์เช่นกัน

4. การแปลงลาปลาซและการแปลงลาปลาซผกผัน (Laplace Transform and Inverse Transform)

ในเนื้อหาแคลคูลัสเบื้องต้นนั้น ได้มีการบรรจุเนื้อหาเกี่ยวกับการหาอนุพันธ์และ การอินทิเกรตของฟังก์ชันไว้ ซึ่งทั้งสองกระบวนนี้เป็นการแปลงเบื้องต้น นั่นคือ แปลงจากฟังก์ชัน หนึ่งเป็นอีกฟังก์ชันหนึ่ง

5. ฟังก์ชันหลายตัวแปรและอนุพันธ์ย่อย (Functions of Several Variables and Partial Derivatives)

ฟังก์ชันหลายตัวแปร (Functions of Several Variables)

สำหรับฟังก์ชัน 2 ตัวแปร จะเขียนแทนด้วย f (x , y) ตัวอย่างเช่น

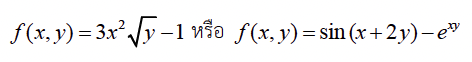
หรือแล้วแต่จะตั้งชื่อ เช่น z = x² y + 2x + y เป็นต้น โดยที่ x, y คือ ตัวแปรต้น (independent variables) และ z คือ ตัวแปรตาม (dependent variable) สำหรับฟังก์ชัน 3 ตัวแปร จะเขียนแทนด้วย f(x, y, z) ในทำนองเดียวกัน ฟังก์ชัน n ตัวแปร จะเขียนแทนด้วย f(x₁,x₂,x₃,…,x_n)

อนุพันธ์ย่อย (Partial Derivatives)

6. ปริพันธ์หลายชั้น (Multiple Integrals)

เนื้อหาในบทนี้จะเป็นการแนะนำการหาปริพันธ์ของฟังก์ชันหลายตัวแปร โดยจะเริ่มแนะนำปริพันธ์สองชั้นก่อน

1. ปริพันธ์สองชั้น

2. ปริพันธ์สามชั้น (Triple Integrals)

7. แคลคูลัสของเวกเตอร์ (Vector Calculus)

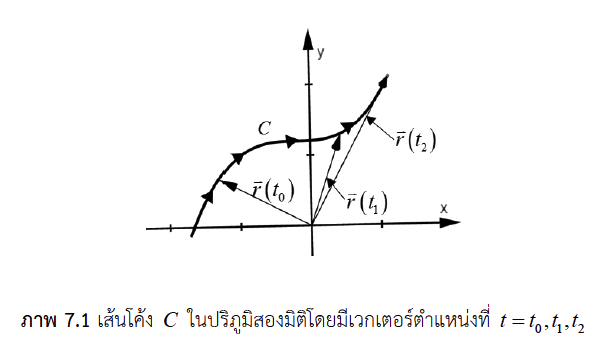
เนื้อหาในส่วนนี้จะเกี่ยวกับการหาอนุพันธ์ ปริพันธ์และการประยุกต์ที่เกี่ยวข้องของ เวกเตอร์ สนามเวกเตอร์ และฟังก์ชันเวกเตอร์ต่าง ๆ

ค่าเวกเตอร์และพีชคณิตของเวกเตอร์ (Calculus of Vector-Valued Functions)

สำหรับหัวข้อนี้จะพูดถึงเวกเตอร์และกระบวนการต่าง ๆ ที่เกี่ยวกับเวกเตอร์ โดยจะเริ่ม ด้วยการแนะนำนิยามพื้นฐานต่าง ๆ ของเวกเตอร์ดังต่อไปนี้

แคลคูลัส 3 (Calculus III) เป็นเนื้อหาขั้นตอนสุดท้ายของแคลคูลัส หนังสือ เล่มนี้แบ่งเป็นสองส่วน ในส่วนแรกเป็นการหาผลเฉลยของสมการเชิงอนุพันธ์เชิงเส้นอันดับหนึ่งและอันดับสูง การใช้ผลการแปลงลาปลาซและลาปลาซผกผันสำหรับการหาผลเฉลยของสมการเชิงอนุพันธ์ สำหรับส่วนที่สองเป็นการหาอนุพันธ์และปริพันธ์ของฟังก์ชันหลายตัวแปรและแคลคูลัสของเวกเตอร์ เช่น ปริพันธ์ตามผิวและทฤษฎีบทของเกาส์และสโตกส์ เป็นต้น ทฤษฎีบทและตัวอย่างในหนังสือเล่มนี้ มีความละเอียดสูงและชัดเจน ซึ่งเหมาะสมกับผู้ที่มีความสนใจแคลคูลัสในทุกระดับ ทุกอาชีพ โดยเฉพาะผู้ที่ต้องการคำปรึกษา ทางด้านแคลคูลัสสามารถศึกษาและเข้าใจได้ด้วยตนเอง